Wskazówka:
Oczywiste jest, że trzy słowa długości 4 nie zmieszczą się w słowie o długości 8, jeśli nie
będą się częściowo nakładały. Wyobraźmy sobie zatem — nie znając jeszcze jego liter —
tekst o długości 8, w którym musi wystąpić trzy razy wzorzec:

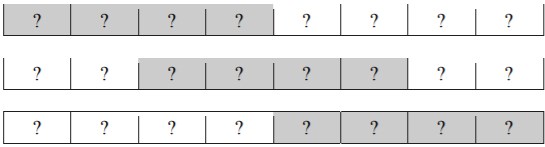
Analogicznie takie same muszą być litery 2, 4, 6 i 8, a to znaczy, że możliwą odpowiedzią do zadania jest na przykład:

Wzorzec abab występuje w nim trzy razy, tak jak zaplanowaliśmy.
Równie dobrze można jednak zamiast liter a i b wybrać na przykład x i y albo nawet a i a — otrzymalibyśmy wtedy tekst aaaaaaaa i wzorzec aaaa, będące również prawidłowym rozwiązaniem (wzorzec występuje w tekście aż pięć razy). Moglibyśmy też inaczej zaplanować wystąpienia wzorca w tekście:

W tym wypadku podobne rozumowanie prowadzi do wniosku, że litery pierwsza, druga itd.
aż do szóstej, muszą być wszystkie identyczne, za to dwie ostatnie mogą być absolutnie dowolne. Otrzymamy w ten sposób kolejne możliwe rozwiązania: wzorzec aaaa i tekst
aaaaaabc.

Wybierzmy miejsca, w które chcemy wpasować wzorzec, na przykład w ten sposób:

Widzimy, że skoro ten sam wzorzec ma wystąpić na miejscach 1 – 4 oraz 3 – 6, to pierwsza
i trzecia litera tekstu muszą być takie same (są pierwszą literą wzorca), podobnie trzecia
i piąta oraz piąta i siódma.
Analogicznie takie same muszą być litery 2, 4, 6 i 8, a to znaczy, że możliwą odpowiedzią do zadania jest na przykład:

Równie dobrze można jednak zamiast liter a i b wybrać na przykład x i y albo nawet a i a — otrzymalibyśmy wtedy tekst aaaaaaaa i wzorzec aaaa, będące również prawidłowym rozwiązaniem (wzorzec występuje w tekście aż pięć razy). Moglibyśmy też inaczej zaplanować wystąpienia wzorca w tekście:
